

Although some translations of Plato's work give the statement that the Atlanteans would meet every fifth and sixth year, one translation explicitly states the fourth and fifth year gathering at their capital seaport.
This historical view is important because if our Atlantean ancestors added a "leap-day" every fourth and fifth year during such "social gatherings" -- together with adding a jubilean "super leap-day" every fifty years to a 365-day solar calendar, the calendrical result would equal the True Tropical Solar Year value of 365.2422 days a year.
Today's Gregorian Calendar -- which replaced the Julian Calendar of 365.25 days a year nearly four centuries ago, equals only 365.242 days a year. Although the Gregorian Calendar is quite accurate, falling short by only one day every 5000 years from the True Tropical Solar Year value, it uses a time counting formula wherein historians must remember not to use the 4-year leap-day rule in century years -- unless the year is divisible by 400.
Remembering not to count the leap-day event every century -- unless the century is divisible by 400, is a time-keeping rule that spans a long time between calendrical events. Many social and environmental factors could make historians forget this somewhat complicated time keeping rule -- in fact, although the calendrical rule can be found in many encyclopedias, most people are probably not even aware that it exist.
For example, if the historical archives and time-keeping habits of Western Civilization were corrupted by a catastrophic environmental event and had to start over again, the 4-year leap-day rule may be remembered by some survivors -- but would the additional rule about not adding a leap-day every century unless it was divisible by 400 be remembered or understood by surviving historians?
So far, the Gregorian Calendar has worked just fine -- but was it the first solar calendar designed to remind time-keepers about leap-day rules beyond the 4-year event?
Perhaps not, because the fourth and fifth year gathering event documented by Plato -- together with other calendrical data, suggest the idea that the Atlanteans once used leap-day rules long before the leap-day rule of even the Julian Calendar.
Conventional history portrays that the astronomer Sosigenes designed the leap-day rule of the Julian Calendar -- however, that calendrical rule became effective about the same time when the Romans met the Armoricans near Brittany.
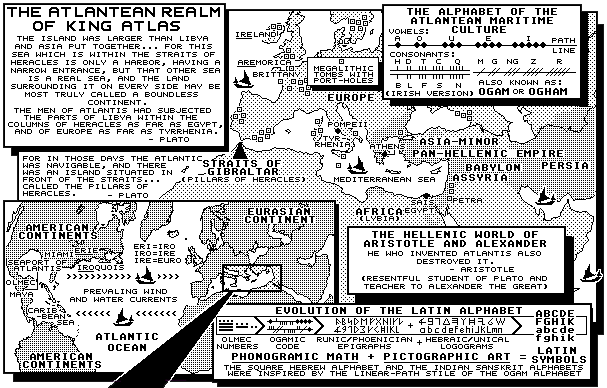
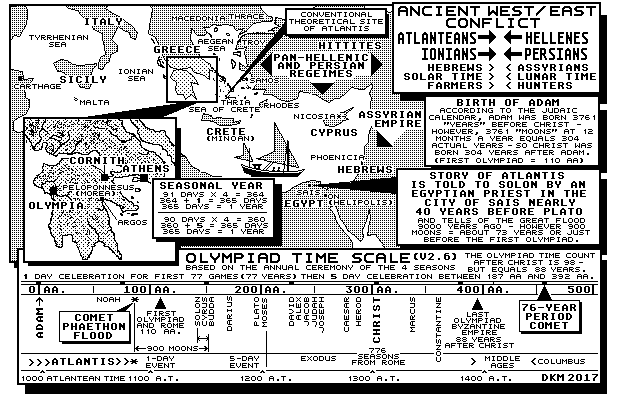
What makes this historical view truly important is that the Romans may have followed a time-keeping habit of the Armorican/Atlantean culture which used leap-day rules to balance calendrical time.
For example, a 7-day weekly counting formula can only add up to 364 days a year. So in order to "balance" a 364-day count to a 365-day year count, our ancestors added an extra "pass over" day -- or a day that was not a week day, but was rather a "year" day to the annual count of time.
The total stairway count of 364 "day-steps" on the main pyramid at Chichen Itza in the Yucatan Peninsula is a good example of how ancient time-keepers used "temple tools" to help keep public time. An ancient "calendar stick" from the British Isles wherein four edges that totaled 364 markings is another example of how annual time was once kept by our ancestors. Both devices allowed for an extra year-day ceremonial event to make a 365-day year.

When it was learned that the solar year needed even more balancing, another extra day formula was a natural decision for time-keepers.
When to inter calculate an extra day count onto a 365-day solar calendar must of taken many years of celestial measuring. Incidentally, the business number symbol "#" probably originated from the "cross-hatch" design of counting and measuring calendrical time within a square grid.
53/ The answer to the first question lies in the realization that a .2422 day, or 5.8128 hours, amounts to the solar-time value of 145.32 "solar units" -- in which a "solar unit", or 144 seconds, is the length of time it takes the sun to completely rise or set at the horizon during the equinoxes.
(There exists exactly 600 "solar units" every 24 hours during the equinoxes in the tropical latitudes; 144 seconds -- or 2 minutes and 24 seconds, times 600 equals 24 hours)
[If there is any question as to why the 60 second and 60 minute time values are used today to keep daily time, the answer lies in the 600 "solar unit value" every 24 hours formula]
54/ In other words, an "optical time measuring device" was once used to detect the exact time value of 145.32 solar units, or 5.8128 hours, between the sunset of the Spring Equinox and the helical setting of the "dog" star Sirius after counting 365 days.
(Using the second brightest star in the sky as a "timing light" in comparison to solar light is very unique in time-keeping techniques)
[Not withstanding this incredible technique in measuring the annual time difference between our setting sunlight and the setting starlight of Sirius -- is the amazing coincidence that the amount of time between a ray of light from our sun and a ray of light from the second brightest star in the sky, equals the same percent value of a solar day that can be found in the leap-day formula of the Trans-Atlantean Solar Calendar]

The time between the setting of the sun and the setting of Sirius
on the Spring Equinox equals 5.8128 hours -- or .2422 of a 24 hour day.
Verified by the Astronomical program Stellarium, the .2422 leap-day formula -- used in the Trans-Atlantean Solar Calendar to "balance calendar timekeeping", was discovered long before the Greco-Roman Era. However, the art of simulating star date activity far in the past using any computer program will have "timing issues" -- resulting in some inconsistant data that may not be fully accurate.

Pyramidal Star Clocks.
56/ So, for every 100 years the .2422 "extra" day would accumulate to the time value of 24.22 "extra" days.
(A .2422 day times 100 equals 24.22 days)
57/ Now because if every 100 years were to be divided by the time value of 4.5 years -- whereby for every alternate fourth and fifth year, an "extra" leap-day was intercalated, the result would amount to 22.22 extra days every 100 years.
58/ Add to this 22.22 extra day formula, one more extra day every 50-years -- or one "super-leap" day, and the total amount would equal 24.22 extra days every 100 years!
Also according to Plato, the reason why the Atlantean maritime kingdom -- and their time-keeping ways, disappeared from history was because of a catastrophic world-wide event that engulfed the trans-continental kingdom.
That catastrophic world-wide event was probably the result of gravitational and atmospheric reactions caused by a rogue comet crashing into the Sun.
In the aftermath of such a major event, the surviving "lost tribes" of the former Atlantean realm regrouped and some calendrical knowledge of the leap-day habit may have appeared as a 4-year leap-day rule of the Julian Calendar and the 50-year Jubilean ceremony of the Old Testamemt.
And speaking of time ceremonial events stories within the Holy Bible, there exist some interesting numerical data in Revalations 21:16 wherein what is supposed to be a hevenly place as measured by an angel, reveal numbers relating to the measurement of time -- such as 144 and 12 -- and 24, 4 and 7.
It seems that there once was a place in heaven where somekind of time-keeping machine or clock existed -- as in 144 seconds equals the "timely size" of the Sun crossing the horizon -- or 24 hours in a day, or 7 days a week -- or 4 seasons a year and 12 months a year.
Speaking of the measurment of solar time, the following image and data suggest there exist some kind of "divine value" between certain time measurements and planetary cycles within our universe.
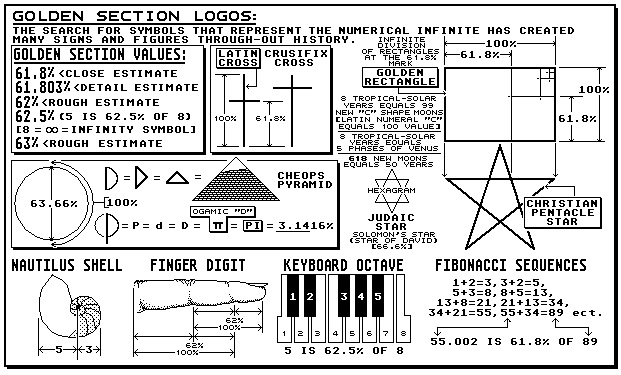
The Golden Section measurement is found in astronomical events.
Moreover, because 618 new Moons equals 50 Tropical-Solar years, the Golden Section value of 61.8% can be found in the timely measurement of light from celestial objects.
And speaking of the timely measurement of light from celestial objects, the planet of Saturn goes around the Sun every 29.4 Earth years -- which is a similar numerical measurement found in the Lunar cycle of how long the Moon phases every 29.5 days around the Earth.
The significance of these numerical values between certain planets and Earth -- and our Moon, may be just a coiencidence -- or there may be some kind of "divine aspect" in how the speed of light and energy moves around in our solar system.
Also, the following images include calendar data once used by the Mayan Civilization in Central America that relate to how they kept time records long ago.


New Mayan timekeeping data.